[問題]
たし算は2つの数から1つの数を求める計算で,3つ以上
の数をたすときには,2つの数のたし算をくり返していくこ
とになります.
たとえば1+2+3や1+2+3+4を,カッコを用いて2つ
のたし算で書き表す方法は,次のようにそれぞれ2通り,5
通りあります.
1+(2+3),(1+2)+3
1+(2+(3+4)),(1+2)+(3+4),((1+2)+3)+4,
1+((2+3)+4),(1+(2+3))+4
[注意] たくさんの数をたす場合も考えて,{ }や[ ]を使わずに( )だけを用いています.
1+(3+2)のように,たす数を並べかえることは考えません.
このような式を完全式と呼ぶことにします.このような書き方になっていない,次のような式などは完全式ではありません.
1+2+3 (3つをたしている)
1+(2+3)+4 (1と(2+3)と4の3つをたしている)
(1+2+3)+4 (1と2と3の3つをたしている)
1+2+3+4 (4つをたしている)
このとき,次の問いに答えなさい.
(1) 1+2+3+4+5には何通りの完全式がありますか.
(2) 1+2+3+4+5+6の完全式のうちで,
1+(2+(3+(4+(5+6))))のように1がカッコに囲まれな
いものは全部で何通りありますか.
(3) 1+2+3+4+5+6の完全式のうちで,
(1+(2+3))+(4+(5+6)))のように3と4の間の+が
カッコに囲まれないものは全部で何通りありますか.
(4) 1+2+3+4+5+6には何通りの完全式がありますか.
(01 洛南高附)
■[解答] ■
(1) ① 1+(2+3+4+5) のタイプ
部へのカッコのつけ方を考えると,
問題文の例の「1+2+3+4」へのカッコ
のつけ方と同じで5通り.
② (1+2)+(3+4+5) のタイプ
部へのカッコのつけ方を考えると,
問題文の例の「1+2+3」へのカッコの
つけ方と同じで2通り.
③ (1+2+3)+(4+5) のタイプ
②と同じ2通り.
④ (1+2+3+4)+5のタイプ
①と同じ5通り.
以上により,5+2+2+5=14 (通り)
(2) 1+(2+3+4+5+6) のタイプだから,
部へのカッコのつけ方を考えると,
(1)の「1+2+3+4+5」へのカッコのつ
け方と同じで14通り.
(3) (1+2+3)+(4+5+6) のタイプ.
2つの 部へのカッコのつけ方は,そ
れぞれ2通りずつあるから,答えは,
2×2=4 (通り)
(4) 1+2+3+4+5+6の完全式には,
(2),(3)以外に,
① (1+2)+(3+4+5+6)
② (1+2+3+4)+(5+6)
③ (1+2+3+4+5)+6
のタイプがある.
部へのカッコのつけ方を考えると,①のタイプは5通り.
②のタイプは,①と同じで5通り.
③のタイプは,(2)と同じで14通り.
以上により,答えは,
14+4+5+5+14=42(通り)
なぜ,“カッコのつけ方”が
「カタラン数」と一致するのか?
たとえば,
㋐ 1+(2+3) や ㋑ (1+2)+3
を日本語に読みくだすと,
㋐ 1+(2+3)
…「1に,2と3をたしたものをたす」
㋑ (1+2)+3
…「1に2をたしたものに,3をたす」
となります.
ここで, 部を順に,数や+ (プラス)
の記号で書き連ねると,
㋐ 1+(2+3) …“123++”
㋑ (1+2)+3 …“12+3+”
となります.
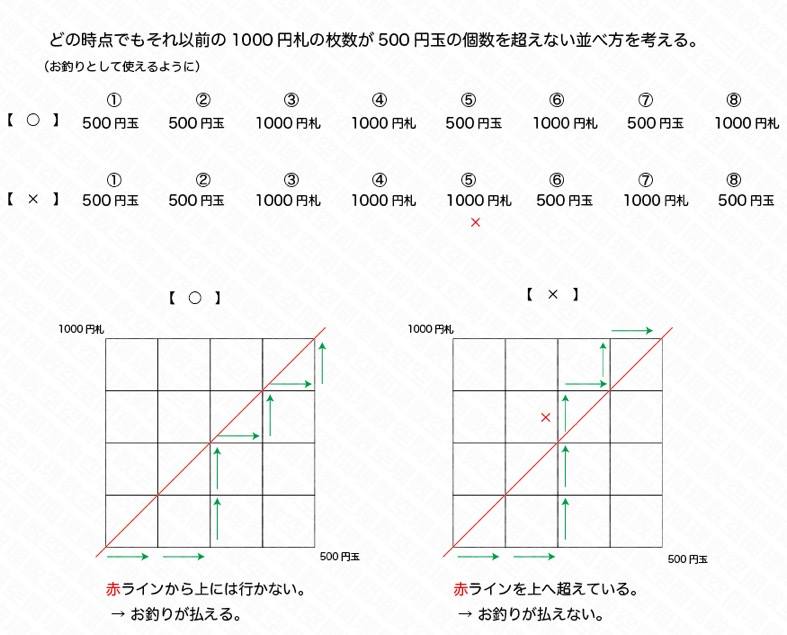
これらの数や+の列を左から順に見ていくと,「数の個数」がいつでも「+の個数」を上回っていますね.
㋑では,
となります.
“+” の記号が現れる前には,必ず“〇と△を”という言い回しがあるはずなので,
「数の個数」がいつでも「+の個数」を上回るのです.
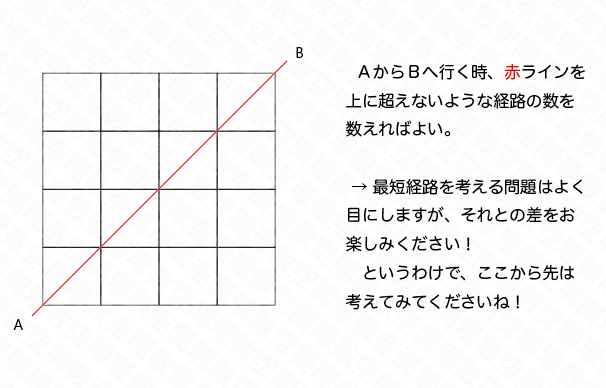
すると,例の経路の数を数える話です.
上の図の 線を上に超えない経路の数を書き込むと,カッコのつけ方の総数が求められるというワケです.
本問の (4) では,数が6個,+が5個ですから,一番右上の,42通りが答えとなります.