2020灘中算数分析

合格者平均点は，第1日(以下，①)が72点，第2日(以下，②)が71点．昨年の①50点，②57点と比べると，大幅に易化しました．昨年度は，あまりにも難しいセットだったため，学内でも問題になったという噂がしきりで，その反動で易しくなったようです．過去5年間でも最も高い平均点です．
実際に，①では，9番を除くと受験生に手が出せないような難問はなく，②でも，最後の5番以外は例年の難易度を下回っています．
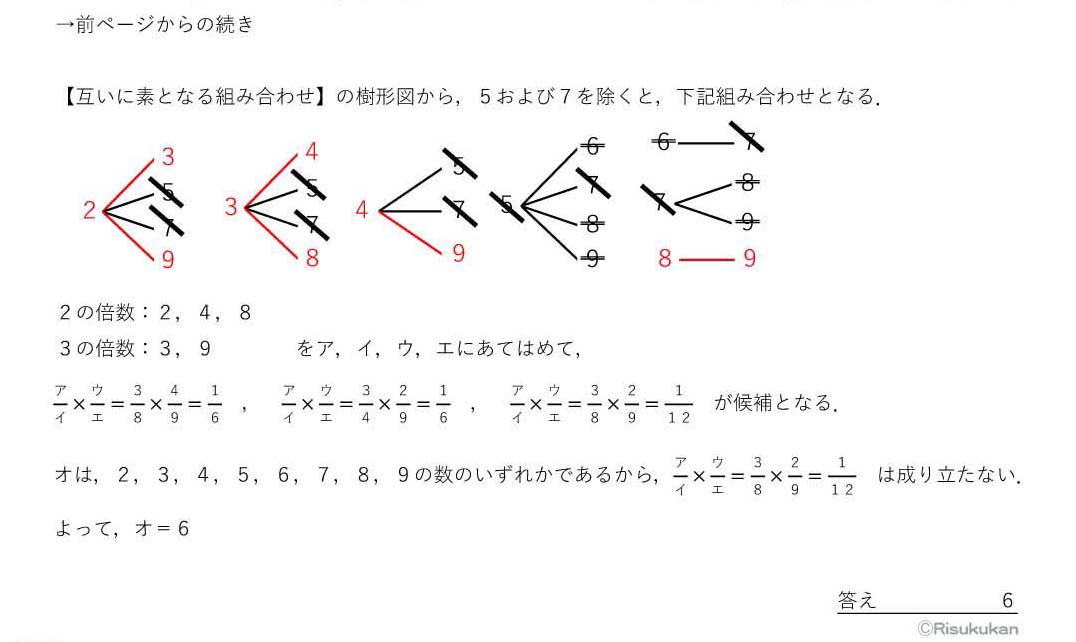
①の5番は，高校数学の‘2項定理’を背景としています(というより，モロ2項定理)．しかし，この定理の本質に触れることなく，表面的な規則性を読み取れさえすれば解けてしまう，つまり，ワケが分からなくても答えは出せるという，灘中の問題としては異例(?)の出題でした．
①の2番，3番，4番，6番，②の1番，2番，3番はいかにも灘中らしい問題ですが，ピカッと光る印象は受けません．
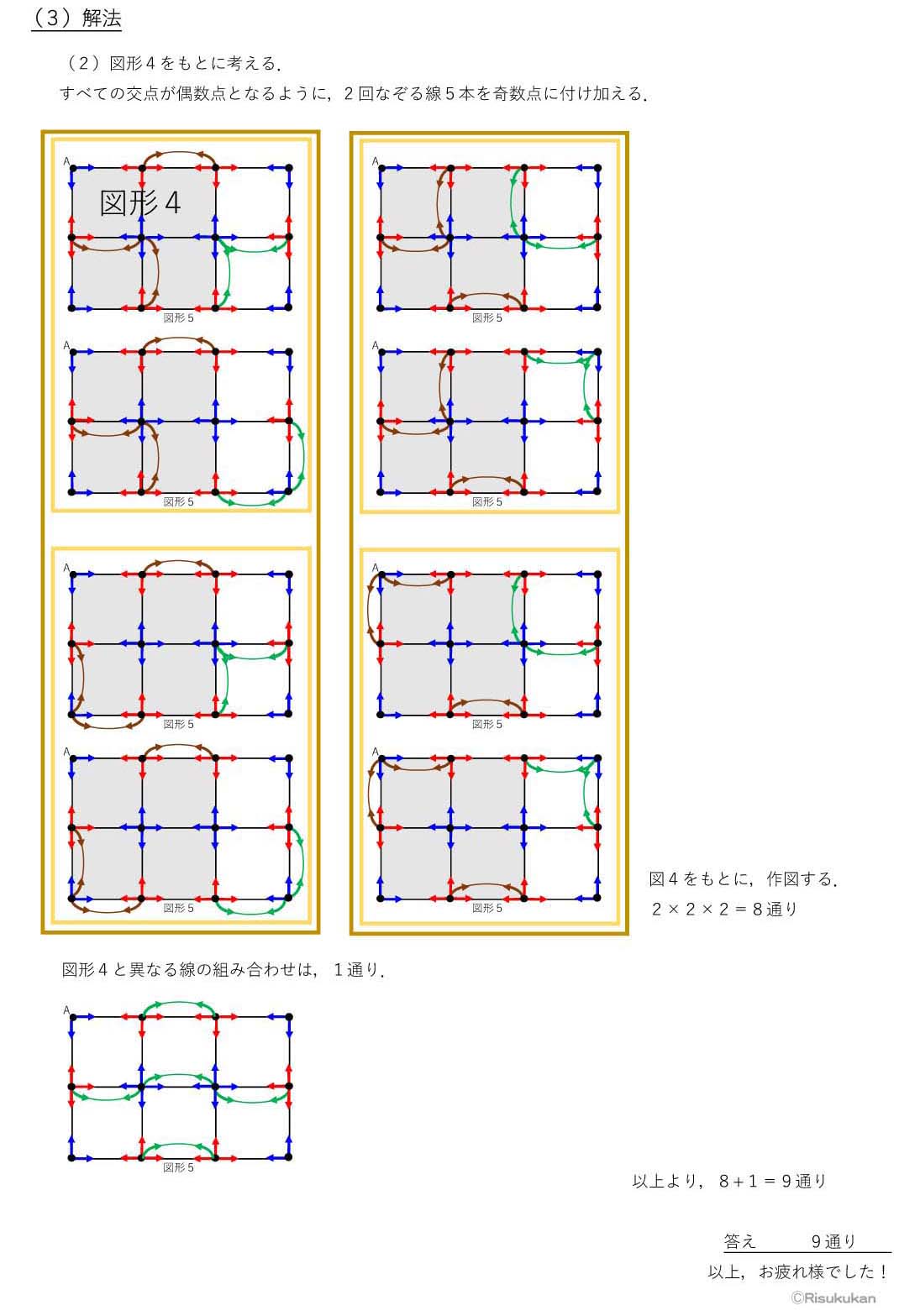
そんな中，①の9番は秀逸でした．理数空間の第16回“お母さんのための「受験の算数・数学」”でとりあげる予定です．台形を分割した図形からこの図形を作ったものと思われますが，単純な図形を組み替えて難問に仕上げる手法は，すばらしい!!の一言です．