■■ 問題 ■■
■■ 問題 ■■ (文字データ)
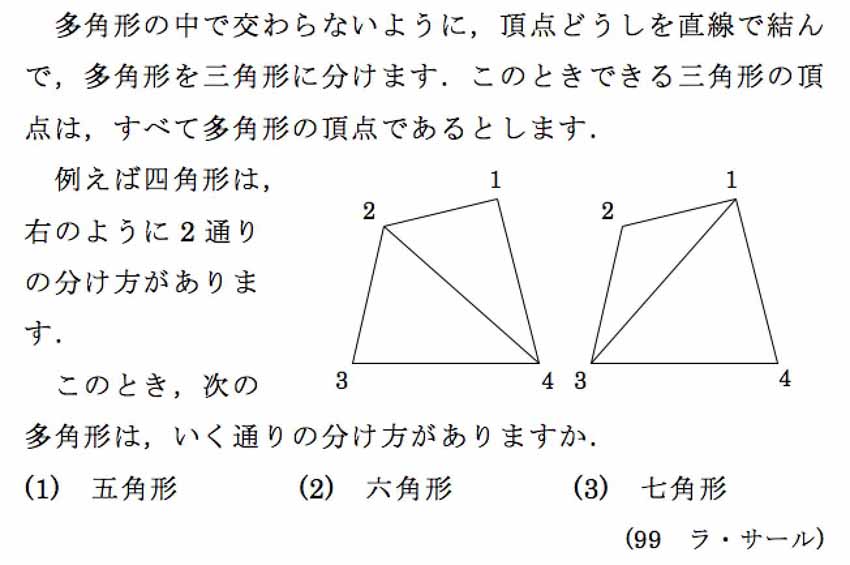
多角形の中で交わらないように、頂点どうしを直線で結んで、多角形を三角形に分けます。このときできる三角形の頂点は、すべて多角形の頂点であるとします。
例えば四角形は、(右の図のように)2通りの分け方があります。
このとき、次の多角形は、幾通りの分け方がありますか。
(1)五角形 (2)六角形 (3)七角形
(99 ラ・サール)
■■ 解答 ■■
ここでは,【他では聞けない『高校への数学』編集長セレクション】/カタラン数Aの“カッコのつけ方”の問題(洛南高附01)と関連付けて解説してみます.
下の図1のような六角形で考えてみましょう.六角形の6つの辺のうち5つに,順にa,b,c,d,eと記号を振っておきます.

次に,図2は条件を満たすような分け方の1つです.分けるときに引いた直線は,①,②,③で,六角形の,記号を付けなかった辺を④とします.

すると図2で,
・①はa,bの辺をつないでいるので,
①=a+b
・②は①,cの辺をつないでいるので,
②=①+c=(a+b)+c
・③はd,eの辺をつないでいるので,
③=d+e
・④は②,③の辺をつないでいるので,
④=②+③=((a+b)+c)+(d+e)
となり,5文字の和a+b+c+d+eの“完全式”の1つができました.異なる分け方をした場合には,異なる完全式ができます.また,すべての完全式から異なる分け方が復元できるので,結局,本問は前問
と同じカタラン数の問題だとわかります.
まとめると,
“n角形の分け方”
=“(n-1)個の数の和の完全式の個数”
です(図1で,辺につけた記号が,辺の数より1つ少なかったことに注意しましょう).
そんなわけで,答えは次の通りです.
(1) 五角形の分け方は,4個の数の和の完全式の個数と同じで,5通り.
(2) 六角形の分け方は,5個の数の和の完全式の個数と同じで,14通り.
(3) 七角形の分け方は,6個の数の和の完全式の個数と同じで,42通り


